선형시간 정렬 알고리즘
- O(n) -> comparison sort가 아님
counting sort
- n개의 정수를 정렬하라. 단 모든 정수는 0에서 k사이의 정수이다. ->데이터의 사전지식이 있음
- ex) n명의 학생들의 시험점수를 정렬하라. 단 모든 점수는 100이하의 양의 정수이다.
ex) k = 5인 경우 ->0~5까지의 숫자가 나온다! , n은 8!
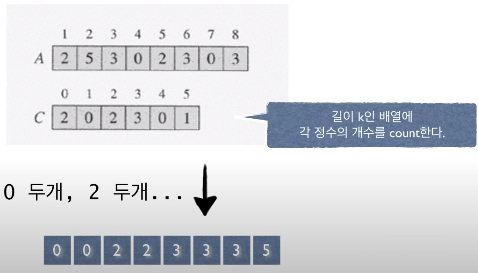
- c라는 배열에는 A배열의 원소를 count하기 위해 만듬

위의 배열 그림을 이렇게 수도코드로 만들수 있다.
하지만 여기에는 문제가 있다. 단순한 배열을 정렬하는 상황이라면 문제가 되지 않겠지만 대부분의 경우 정렬한 값들은 레코드의 key값이기 때문에 위의 수도코드 방식으로 정렬하면 레코드의 값들을 정렬할 수 없다.
따라서 다른 방법을 찾아야 한다.

a) A배열의 원소를 원래 방법대로 C배열에 옮긴 형태이다.
b) 이번 C 배열에는 좀 다르게 원소값을 입력하는데 C배열의 index값 이하로 몇개 있는지를 C배열의 원소로 입력한다. 예를 들어 3같은 경우에는 0이 2개, 1이 0개, 2가 2개, 3이 3개이므로 7을 입력해준다.
c) A배열을 봤을때 마지막 원소가 3이다. 그리고 다시 만든 C배열을 보면 3은 7을 갖고있다. 이 뜻은 7번 자리에는 무조건 3이 올수 있다는 뜻이다. 따라서 새로운 배열 B에 7번자리에 3을 넣어주고 C배열의 3자리에 -1을 해주면 된다.
d) 다시 A배열을 보면 뒤에서부터 3다음에 0이 나온다. 배열 C에서 0은 2를 나타내므로 B배열 2에 0을 넣어주고 C배열의 0자리에 -1을 해주면 된다.
e) 그 다음 수 3을 가지고 반복해준 것이다.

위의 그림에 대한 수도코드 이다.
1,2번은 k만큼, 3,4번ㄴ은 n만큼, 6,7번은 k만큼, 9,10,11번은 n만큼 반복한다.
즉 k+n+k+n의 시간복잡도를 갖게 되는 것이다.
--> O(2k+2n) = O(k+n) 대부분의 경우 k가 n보다 작다(k가 클 경우 비실용적) ==> O(n)
- 이 같은 방법의 알고리즘을 Stable 정렬 알고리즘 이라고 한다
stable 정렬 알고리즘 - 입력에 동일한 값이 있을 때 입력에 먼저 나오는 값이 출력에서도 먼저 된다.
- counting정렬은 stable하다.
Radix Sort
- n개의 d자리 정수들
- 가장 낮은 자리수부터 정렬

- 매 단계에서 Stable sort를 사용
- 매 단계에서 counting sort가 적합

A배열과 d자리수를 매개변수로 받는다.
- d번 반복하고 반복하면서 counting sort사용
시간복잡도 -> O(d(n+k)) -> 대부분 n이 k보다 크다 O(d(n)) -> d또한 정해진 상수라고 생각한다면 O(n)이 된다.
지금껏 공부해온 정렬들의 시간복잡도 입니다!!

* 위의 그림들은 "영리한 프로그래밍을 위한 알고리즘" 강좌에서 가져왔습니다.
'알고리즘' 카테고리의 다른 글
| 이진검색트리-1 (0) | 2021.03.07 |
|---|---|
| 트리와 이진트리 (0) | 2021.03.07 |
| 정렬의 lower bound (0) | 2021.03.01 |
| 힙(heap)의 용용 : 우선순위 큐(priority queue) (0) | 2021.03.01 |
| Heap_sort(힙 정렬) [java] (0) | 2021.02.28 |




댓글