comparison sort
- 데이터들간의 상대적 크기관계만을 이용해서 정렬하는 알고리즘
- 따라서 데이터들간의 크기 관계가 정의되어 있으면 어떤 데이터에든 적용가능(문자열, 알파벳, 사용자 정의 객체 등)
- 버블소트, 삽입정렬, 합병정렬, 퀵소트, 힙정렬 등
non-comparison sort
- 정렬한 데이터에 대한 사전지식을 이용 - 적용에 제한
- bucket sort
- radix sort
** 오늘 정리할 내용
qucik sort, heap sort, merge sort에서 평균 시간복잡도는 O(nlogn)이다. 여기서 O(nlogn)보다 더 작은 시간복잡도는 불가능한가?에 대한 내용이다.
결론부터 말한다면 comparison sort에서는 불가능하다.
하한(lower bound) : 특정 정렬의 하한이 정해지면 그 시간복잡도보다 작은 알고리즘은 존재하지 않는다는 의미
- 입력된 데이터를 한번씩 다 보기 위해서 최소 O(n)의 시간복잡도가 필요
- 합병정렬과 힙정렬 알고리즘들의 시간복잡도는 O(nlogn)
- 어떤 comparison sort알고리즘도 O(nlogn)보다 나을수 없다.
Decision Tree
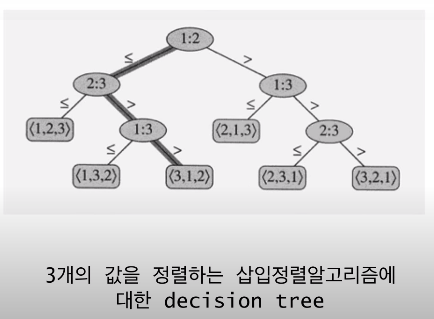
- 그림의 숫자는 index를 가리킨다 -> 처음에는 1번과 2번을 비교하고 그 결과에 따라 3번과 비교한다.
위에 그림으로 이해할때
n개의 원소를 decision tree로 봤을 때 leaf노드의 개수는 n!이 된다. n개의 원소를 줄세우는 것이기 때문이다.
leaf노드가 n!이 되기 위해서는 트리의 계층이 최소한 logn!이 되어야 한다.
stirling's formula를 이용하면 logn! = nlogn이 됨을 알 수 있다.
따라서 아무리 시간을 줄이려고 해도 nlogn보다 밑으로 줄일수는 없다.
'알고리즘' 카테고리의 다른 글
| 트리와 이진트리 (0) | 2021.03.07 |
|---|---|
| sorting in linear time (0) | 2021.03.02 |
| 힙(heap)의 용용 : 우선순위 큐(priority queue) (0) | 2021.03.01 |
| Heap_sort(힙 정렬) [java] (0) | 2021.02.28 |
| quick_sort(퀵 정렬) [java] (0) | 2021.02.25 |




댓글