최단경로
- 가중치 (방향) 그래프 G=(V,E), 즉 모든 에지에 가중치가 있음
- 경로 p=(v0,v1,....vk)의 길이는 경로상의 모든 에지의 가중치의 합
- 노드 u에서 v까지의 최단경로의 길이를 ∂(u,v)라고 표시하자 ==> 최단경로를 공부하는 목적
최단경로문제의 유형
- single-source :
- 하나의 출발 노드 s로부터 다른 모든 노드까지의 최단 경로를 찾아라.
- 예 : Dijkstra의 알고리즘
- single-destination :
- 모든 노드로부터 하나의 목적지 노드까지의 최단 경로를 찾아라.
- single-source 문제와 동일
- single-pair : one-to-one
- 주어진 하나의 출발 노드 s로 부터 하나의 목적지 노드 t까지의 최단 경로를 찾아라
- 최악의 경우 시간복잡도에서 single-source 문제보다 나은 알고리즘이 없음
- all-pairs :
- 모든 노드 쌍에 대해서 최단 경로를 찾아라.
최단경로와 음수 가중치
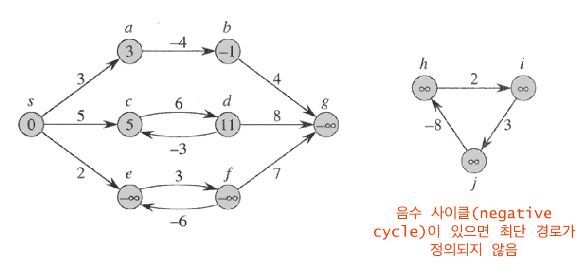
- 알고리즘에 따라 음수 가중치가 있어도 작동하는 경우가 있고 그렇지 않은 경우도 있음
최단경로의 기본 특성
- 최단 경로의 어떤 부분경로도 역시 최단 경로이다.
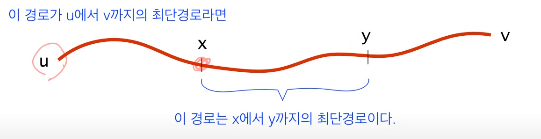
u,v의 최단경로 중 x,y가 있다면 x,y의 최단 경로가 된다.
- 최단 경로는 사이클을 포함하지 않는다.(음수 사이클이 없다는 가정하에서)
single-source 최단경로문제
- 입력 : 음수 사이클이 없는 가중치 방향그래프 G=(V,E)와 출발 노드 s∈V
- 목적 : 각 노드 v∈V에 대해서 다음을 계산한다.
- d[v]
* 처음에는 d[s]=0, d[v]= ∞ 로 시작한다.
* 알고리즘이 진행됨에 따라서 감소해간다. 하지만 항상 d[v]≥∂(s,v)를 유지한다
* 최종적으로는 d[v]=∂(s,v)가 된다.
- ∏[v] : s에서 v까지의 최단경로상에서 v의 직전 노드(predecessor)
* 그런 노드가 없는 경우 ∏[v] = NIL.
기본 연산 : Relaxation

single-source 최단경로
- 대부분의 single-source 최단경로 알고리즘의 기본 구조
1. 초기화 : d[s]=0, 노드 v != s에 대해서 d[v]=∞, ∏[v] = NIL.
2. 에지들에 대한 반복적인 relaxation
- 알고리즘들 간의 차이는 어떤 에지에 대해서, 어떤 순서로 relaxation을 하느냐에 있음
기본 알고리즘
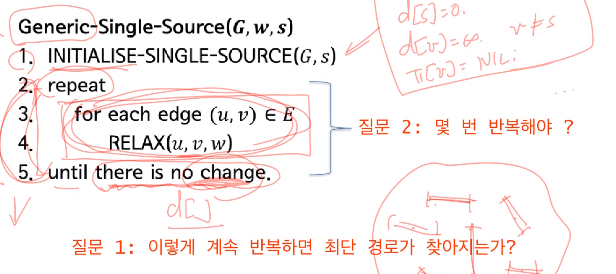
- 질문 2의 답 : n-1번 반복이면 충분하다.
Bellman-Ford 알고리즘

'알고리즘' 카테고리의 다른 글
| 최단경로 - 3 (0) | 2021.03.30 |
|---|---|
| 최단경로 - 2 (0) | 2021.03.30 |
| 최소비용신장트리 - 4 (0) | 2021.03.24 |
| 최소비용신장트리 - 3 (0) | 2021.03.24 |
| 최소비용신장트리 -2 (0) | 2021.03.24 |




댓글