그래프 순회(Graph Traversal)
- 순회 : 그래프의 모든 노드들을 방문하는 일
- 대표적 두 가지 방법
- BFS (Breadth-First search, 너비우선순회)
- DFS ( Depth-First Search, 깊이우선순회)
너비우선순회(BFS)
- BFS 알고리즘은 다음 순서로 노드들을 방문
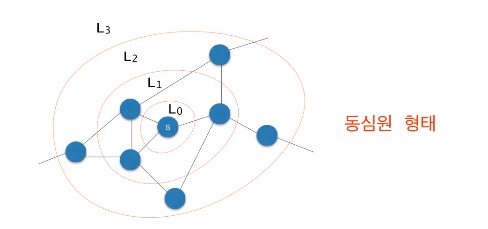
- L0 = {s}, 여기서 s는 출발 노드
- L1 = L0의 모든 이웃 노드들
- L2 = L1의 이웃들 중 L0에 속하지 않는 노드들
- .....
- Li = Li-1의 이웃들 중 Li-2에 속하지 않는 노드들
큐를 이용한 너비우선순회

-큐가 빌때까지 반복
- 탐색이 된 노드는 큐에서 제거
- 그 이웃한 노드들 큐에 삽입 후 방문했다고 체크

- 큐에 1을 넣는다 | 1
- 1을 제거하면서 큐에 인접한 2,3을 넣고 2,3을 방문했다고 체크 | 2,3
- 2를 제거하며 큐에 4,5를 넣고 방문했다고 체크 | 3,4,5
- 3을 제거하는데 인접한 노드는 5,7,8하지만 이전 단계에서 5가 방문됐다고 체크했으므로 7,8만 큐에 삽입
| 4,5,7,8
- 4를 제거하는데 방문하지않은 인접 노드가 없으므로 큐에 넣지않는다 | 5,7,8
- 5를 제거하면서 방문하지않은 인접 노드 6을 삽입 | 7,8,6
- 이제 순서대로 7,8,6을 방문하면 된다
=> 1,2,3,4,5,7,8,6 방문
BFS와 최단경로
- s에서 Li에 속한 노드까지의 최단 경로의 길이는 i이다.
- BFS를 하면서 각 노드에 대해서 최단 경로의 길이를 구할 수 있다.
- 입력 : 방향 혹은 무방향 그래프 G=(V,E), 그리고 출발노드 S<V
- 출력 : 모든 노드 V에 대해서
- d[v] = s로 부터 v까지의 최단 경로의 길이(에지의 개수)
- 파이[v] = s로부터 v까지의 최단경로상에서 v직전의 노드(predecessor)

위의 설명에서 달라진 부분은 s에서 v까지의 최단경로를 넣어주는 부분과 그 직전의 노드를 넣어주는 부분이 생겼다는 것이다.
- while문을 반복할 때 최대 n번 반복되고
- 다음 for문에서 인접행렬로 구현하면 n번 연결리스트로 구현하면 degree(v)번 반복한다.
따라서 그래프가 매우 많이 연결되어 있지않는다면 연결리스트로 구현하는 것이 시간복잡도에서 더 효과적이다.

1을 시작으로 그래프를 순회할 때 최단거리와 직전의 노드를 표현한 그림이다.
너비우선순회 : 최단 경로 출력하기

- s와 v가 같으면 그대로 출력
- v의 직전값이 null이면 s에서 v로 가는 길이 없다.
- v를 출력하면서 s에 도달할 때까지 반복해준다.
** 그래프가 disconnected이거나 혹은 방향 그래프라면 BFS에 의해서 모든 노드가 방문되지 않을 수도 있음
- BFS를 반복하여 모든 노드 방문

- BFS-ALL을 사용하여 모든 노드들을 다 방문
- 방문되지 않았다면 방문한다
* 위의 그림들은 "영리한 프로그래밍을 위한 알고리즘" 강좌에서 가져왔습니다.
'알고리즘' 카테고리의 다른 글
| 그래프 알고리즘 - 4 (0) | 2021.03.17 |
|---|---|
| 그래프 알고리즘 - 3 (0) | 2021.03.17 |
| 그래프 알고리즘 - 1 (0) | 2021.03.16 |
| hashing - 마지막 (0) | 2021.03.11 |
| 이진검색트리-3 (0) | 2021.03.08 |




댓글