quick_sort
개념
- 앞서 설명한 merge_sort랑 마찬가지로 분할정복법을 사용하는 정렬이다.
- 분할 : 배열을 pivot을 기준으로 작은 값들은 왼쪽으로 큰 값은 오른쪽으로 나눈다. , pivot값은 맨 마지막 값으로 한다.
- 정복 : 각 부분을 순환적으로 정렬한다. ->partition
- 합병 : 정복하면서 정렬되므로 따로 합병을 해주지 않아도 된다.
분할
- partition을 통해 pivot의 위치를 리턴받고 그 값을 기준으로 두 개의 분할 메서드를 다시 호출한다.
public static int[] quickSort(int[] base,int p,int r){
if(p<r){
int q = partition(base,p,r);
base = quickSort(base,p,q-1);
base = quickSort(base,q+1,r);
}
return base;
}
정복

* 정복을 쉽게 이해하기 위한 그림이다.
- 현재 pivot의 값은 x이고 pivot보다 작은 값은 index값이 처음부터 i까지이고 큰 값은 i+1부터 j-1까지이다.
- 현재 검사하려는 값이 j인데 만약 이 값이 pivot보다 크다면 j만 1증가시키면 된다.
- 반대로 현재 검사하려는 값이 pivot보다 작으면 i를 1증가시키고 j랑 교환시키고 j를 1증시키면 된다.
- 마지막으로 i가 가리키는 값이 pivot보다 작은 값이고 i+1부터는 다 pivot보다 큰 값이므로 i+1과 pivot값을 서로 교환해야 한다.
public static int partition(int[] base,int p,int r){
int pivot = base[r];
int i = p-1;
for(int j=p;j<r;j++){
if(base[j] <pivot){
i++;
int tmp = base[j];
base[j] = base[i];
base[i] = tmp;
}
}
int tmp = base[r];
base[r] = base[i+1];
base[i+1] = tmp;
return i+1;
}전체 코드
package sort;
import java.util.Arrays;
public class quick_sort {
public static void main(String[] args) {
int[] base= {5,2,4,7,1,3,2,6};
base = quickSort(base, 0,base.length-1);
System.out.println(Arrays.toString(base));
}
public static int[] quickSort(int[] base,int p,int r){
if(p<r){
int q = partition(base,p,r);
base = quickSort(base,p,q-1);
base = quickSort(base,q+1,r);
}
return base;
}
public static int partition(int[] base,int p,int r){
int pivot = base[r];
int i = p-1;
for(int j=p;j<r;j++){
if(base[j] <pivot){
i++;
int tmp = base[j];
base[j] = base[i];
base[i] = tmp;
}
}
int tmp = base[r];
base[r] = base[i+1];
base[i+1] = tmp;
return i+1;
}
}
시간복잡도
최선 - nlogN
최악 - n^2
우선 최악의 경우를 먼저 본다면
고른 pivot이 배열에서 가장 크거나 가장 작은 값이다.
이런 경우는 이미 정렬되어 있는 배열에서 pviot값을 맨 끝값이나 맨 처음 혹은 정렬되어있지 않은 배열에서 임의로 골랐을 때 처음부터 끝까지 가장 큰 값이나 작은 값을 골랐을 때이다.
T(n) = T(0) + T(n-1) + O(n)
= T(n-1) + O(n)
= T(n-2) + T(n-1) + O(n-1) + O(n)
......
= O(1) + O(2) + ....... + O(n-1) +O(n)
= O (n^2)
그럼 반대로 최선의 경우를 생각해보자
이 경우는 merge_sort랑 매우 유사한데 우연히 고른 pivot이 배열의 가운데 값일 경우이다.
T(n) = T(n/2) + T(n/2) + O(n)
= T(n/4) + T(n/4) + T(n/4) + T(n/4) + O(n) + O(n)
....
= O(nlogn)
그런데 여기서 생각해 봐야 할 것이 있다.
최악의 경우의 경우 만약 원소가 10개라면 0 : 10 이렇게 원소가 나뉘는 경우이다. 하지만 이런 극단적인 경우는 극히 드물것이다. 그렇다면 1:9정도로 분할이 된다면 시간 복잡도는 어떻게 될까?
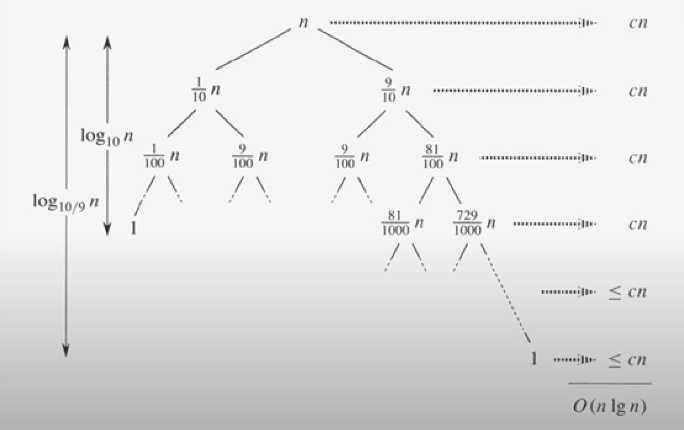
위에 그림은 1:9로 배열을 계속 분할할 경우를 보여준다.
1인부분이 계속되면 n이 logn만큼 반복된다
마찬가지로 9인 부분이 계속 반복된다면 밑이 10/9인 logn만큼 반복된다. 물론 이때는 1인 부분은 이전에 정렬이 되었으므로 n보다는 작은 수가 걸릴 것이다. 하지만 n보다 작지만 이는 상수이므로 무시될수 있다.
따라서 cn이 밑이 10/9인 logn만큼 반복된다. 밑이 10/9는 수학적 계산으로 상수로 빼낼수 있으므로
시간복잡도는 o(nlogn)이 된다.
물론 n이 어마어마하게 커질 경우 nlogn의 시간 복잡도가 나오게 되겠지만 최악의 경우만 아니라면 nlogn의 시간 복잡도를 갖게 된다. 즉 많은 경우의 빠른 정렬이 가능한 것이다.
** 위의 그림들은 "영리한 프로그래밍을 위한 알고리즘" 강좌에서 가져왔습니다.
'알고리즘' 카테고리의 다른 글
| 힙(heap)의 용용 : 우선순위 큐(priority queue) (0) | 2021.03.01 |
|---|---|
| Heap_sort(힙 정렬) [java] (0) | 2021.02.28 |
| merge_sort(합병 정렬)[java] (0) | 2021.02.24 |
| 기본적인 알고리즘 - selection sort (0) | 2021.02.22 |
| 캐시 교체 알고리즘 (0) | 2021.01.23 |



댓글